scipy数值优化与参数估计

车厘子V 2018-08-06

展开全文

引言

优化是一门大学问，这里不讲数学原理，我假设你还记得一点高数的知识，并且看得懂python代码。

关于求解方程的参数，这个在数据挖掘或问题研究中经常碰到，比如下面的回归方程式，是挖掘算法中最简单最常用的了，那么怎么求解方程中的各个参数呢？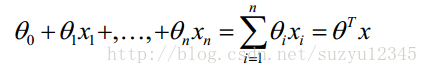

这里写图片描述

当然，对于常见的挖掘算法，甚至是复杂的深度学习，在sklearn和tensorflow等工具已经很好解决怎么求解参数的问题，只需要调接口就好了。
那么我们再看下面的bass方程式，同样很简单，但是没有现成可用的程序可用，怎么求解最优的参数呢？

这里写图片描述

图片不是很清晰，只是为了说明问题。就是如果你有了明确的数学表达式，也有了一些测量数据，怎么求解里面的参数，才是这批文章要说的。

关于求导

其实关于参数求解的方法，是有很标准的方法的，比如最大似然估计，最小二乘法等。这些需要你还记得高数的知识。求导，梯度，然后梯度下降，多么标准的方法啊，这种思想和方法在大部分的数据挖掘算法里面都是这么干的，而且经过精巧而优美的变化，大部分问题总能将目标函数最小化转成凸优化问题。

但是在学习中总不是那么顺利的，除了一些常见的算法可以调程序外，很多研究公式还是要自己想办法求解方程参数，特别是很多论文中，作者为了显示自己研究的独到之处，总是对标准方程加以改造，加入正则项，修正项等等，比如上面的bass方程式，这就尴尬了。
当然，这也可以通过极大似然估计，或者最小二乘的方法，但是不是我们想要的，为什么，因为我们不是搞研究的啊，在工作中，基本就是拿来就用，不行就扔。

scipy数值优化

其实使用scipy进行数值优化，就是黑盒优化，我们不依赖于我们优化的函数的算术表达式。注意这个表达式通常可以用于高效的、非黑盒优化。

scipy中的optimize子包中提供了常用的最优化算法函数实现。我们可以直接调用这些函数完成我们的优化问题。optimize中函数最典型的特点就是能够从函数名称上看出是使用了什么算法。

下面optimize包中函数的概览：

1.非线性最优化

fmin – 简单Nelder-Mead算法
fmin_powell – 改进型Powell法
fmin_bfgs – 拟Newton法
fmin_cg – 非线性共轭梯度法
fmin_ncg – 线性搜索Newton共轭梯度法
leastsq – 最小二乘

2.有约束的多元函数问题

fmin_l_bfgs_b —使用L-BFGS-B算法
fmin_tnc —梯度信息
fmin_cobyla —线性逼近
fmin_slsqp —序列最小二乘法
nnls —解|| Ax - b ||_2 for x>=0

3.全局优化

anneal —模拟退火算法
brute –强力法

4.标量函数

fminbound
brent
golden
bracket

5.拟合

curve_fit– 使用非线性最小二乘法拟合

6.标量函数求根

brentq —classic Brent (1973)
brenth —A variation on the classic Brent（1980）
ridder —Ridder是提出这个算法的人名
bisect —二分法
newton —牛顿法
fixed_point

7.多维函数求根

fsolve —通用
broyden1 —Broyden’s first Jacobian approximation.
broyden2 —Broyden’s second Jacobian approximation
newton_krylov —Krylov approximation for inverse Jacobian
anderson —extended Anderson mixing
excitingmixing —tuned diagonal Jacobian approximation
linearmixing —scalar Jacobian approximation
diagbroyden —diagonal Broyden Jacobian approximation

8.实用函数

line_search —找到满足强Wolfe的alpha值
check_grad —通过和前向有限差分逼近比较检查梯度函数的正确性

参考网上资料，以及从scipy的文档找到的，还有一些没有放上去，这么多，我也没完全搞明白，这里主要讲leastsq和fmin_l_bfgs_b，但是它们的用法基本是一样的。

注意：
1.需要特别说明一点的是，上面的方法，既可以用来求函数的极值，也可以反过来看问题，将参数当做输入变量X，从而在观测样本上计算极值，就是我们要求的参数值。

2.我们下面只讲怎么求解参数，关于用scipy.optimize 求极值的例子很多，官网文档的例子也很好理解，而求解参数的反而没多少，这促使我要把最近的一些学习成果好好整理一下，算是做笔记吧。

3.要时刻记住，当你使用scipy.optimize 的时候，你是使用黑盒优化，你不知道你的目标函数是不是凸函数，也不知道它计算的数值梯度和解析梯度相差有多大，甚至，当你猜的初值不合理，结果也是有问题的。

4.无论如何，你都需要给出误差计算方法，也就是说，你需要知道 $y = f (x)$ 的具体公式是上面，这样才能通过x计算y_hat，通过y_hat和y计算最后的误差residuals。

参数求解步骤

首先是将数据整理成
$输入 X - > 输出 y$
的一一对应关系，这一步看似简单，其实也是最难的，特别是在时间序列这样的函数式里面，
定义需要最小化的目标函数
$r e s i d u a l s . f u n (X)$
最后是调用 leastsq() ,fmin_l_bfgs_b()或其他最小化目标函数
$m i n . r e s i d u a l s . f u n c (X)$

最小二乘 leastsq

最小二乘的思想很好理解，就是找到一组参数，使得函数的拟合值和真实值之间的均方误差最小。
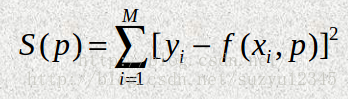这里写图片描述

在学习多元回归和逻辑回归的时候，参数求解，就是通过推误差进行梯度推导，最后进行随机梯度下降来计算的。
我们这里没那么复杂，直接使用 scipy.optimize.leastsq 对误差函数进行最小化即可求出参数值。

# 使用 leastsq 函数求参数，拟合的函数形式是：
# y=A*sin(2*pi*k*x + theta)

# 
import numpy as np
from scipy.optimize import leastsq

def func(x, p): 
    """ 数据拟合所用的函数: A*sin(2*pi*k*x + theta) """
    A, k, theta = p
    return A*np.sin(2*np.pi*k*x+theta)

def residuals(p, y, x): 
    """ 实验数据x, y和拟合函数之间的差，p为拟合需要找到的系数 """
    return y - func(x, p)

# 生成输入数据X和输出输出Y
x = np.linspace(-2*np.pi, 0, 100)       # x
A, k, theta = 10, 0.34, np.pi/6         # 真实数据的函数参数
y0 = func(x, [A, k, theta])             # 真实数据
y1 = y0 + 2 * np.random.randn(len(x))   # 加入噪声之后的实验数据

# 需要求解的参数的初值，注意参数的顺序，要和func保持一致
p0 = [7, 0.2, 0] 

# 调用leastsq进行数据拟合, residuals为计算误差的函数
# p0为拟合参数的初始值
# args为需要拟合的实验数据，也就是，residuals误差函数
# 除了P之外的其他参数都打包到args中

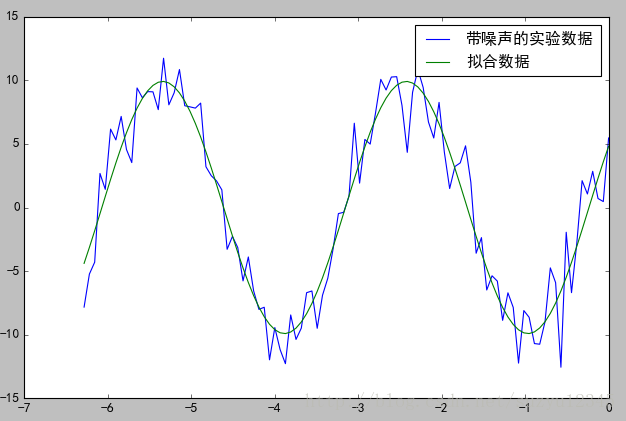
plsq = leastsq(residuals, p0, args=(y1, x)) 

# 除了初始值之外，还调用了args参数，用于指定residuals中使用到的其他参数
# （直线拟合时直接使用了X,Y的全局变量）,同样也返回一个元组，第一个元素为拟合后的参数数组；

# 这里将 (y1, x)传递给args参数。Leastsq()会将这两个额外的参数传递给residuals()。
# 因此residuals()有三个参数，p是正弦函数的参数，y和x是表示实验数据的数组。

# 拟合的参数
print("拟合参数", plsq[0])
# 拟合参数 [ 10.6359371    0.3397994    0.50520845]
# 发现跟实际值有差距，但是从下面的拟合图形来看还不错，说明结果还是 堪用 的。

# 顺便画张图看看1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

这里写图片描述

l-bfgs-b

bfgs算法很厉害啊， BFGS算法是使用较多的一种拟牛顿方法，是由Broyden，Fletcher，Goldfarb，Shanno四个人分别提出的，故称为BFGS校正，BFGS算法被认为是数值效果最好的拟牛顿法，并且具有全局收敛性和超线性收敛速度。

废话不多说，这里也不讲原理了，上例子吧。

# 1

Non-Linear Least-Squares Fitting

在查 scipy.optimize资料的时候，发现了 lmfit，其官网资料也说了，这个模块是对scipy.optimize的封装，使其更加好用。lmfit的资料更加齐全，也有很多例子，在看lmfit的时候，对scipy.optimize的理解更加深刻了。

如果只是简单地说，lmfit对scipy.optimize的待求解参数进行了字典方式的包装，即使在外面改了东西，里面的计算逻辑不需要修改，或者将改动降低到最小。
具体的使用方法，和scipy.optimize也很相似，或者说基本一致吧。

下面是一个简单的例子：

from lmfit import minimize, Parameters

def residual(params, x, data):
    # 误差函数
    amp = params['amp']
    pshift = params['phase']
    freq = params['frequency']
    decay = params['decay']
    model = amp * sin(x * freq  + pshift) * exp(-x*x*decay)
    return (data-model)

# 定义待求解的参数，以及初值，参数的数值范围
params = Parameters()
params.add('amp', value=10, vary=False)
params.add('decay', value=0.007, min=0.0)
params.add('phase', value=0.2)
params.add('frequency', value=3.0, max=10)

# 生成输入x和输出y
x = np.linspace(0, 15, 301)
data = (5. * np.sin(2 * x - 0.1) * np.exp(-x*x*0.025) +
        np.random.normal(size=len(x), scale=0.2) )

# 求解参数
out = minimize(residual, params, args=(x, data), method ='leastsq')

out.params
Parameters([('amp', <Parameter 'amp', value=10 (fixed), bounds=[-inf:inf]>),
            ('decay', <Parameter 'decay', value=0.09861 +/- 0.00626, bounds=[0.0:inf]>),
            ('phase', <Parameter 'phase', value=-0.27096 +/- 0.0399, bounds=[-inf:inf]>),
            ('frequency', <Parameter 'frequency', value=2.06691 +/- 0.0262, bounds=[-inf:10]>)])1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

注意：
lmfit 要求除了leastsq外，其他的优化方法均要求 residual函数返回的是list或者array，而不知一个值，即要求返回的不是 $（ y - y h a t)^{2}$ ，而是np.array或者list，即 $(y - y h a t)$ ，而且list的元素个数不能少于待求解参数的个数。在例子中，residual返回的是 (data-model)。

lmfit支持的优化方法

由于lmfit是对scipy.optimize的包装，所以scipy支持的优化方法lmfit中也支持，通过method参数指定。

lmfit支持的优化方法如下：

method (str, optional) –
Name of the fitting method to use. Valid values are:

leastsq: Levenberg-Marquardt (default)
least_squares: Least-Squares minimization, using Trust Region Reflective method by default
differential_evolution: differential evolution
brute: brute force method
nelder: Nelder-Mead
lbfgsb: L-BFGS-B
powell: Powell
cg: Conjugate-Gradient
newton: Newton-Congugate-Gradient
cobyla: Cobyla
tnc: Truncate Newton
trust-ncg: Trust Newton-Congugate-Gradient
dogleg: Dogleg
slsqp: Sequential Linear Squares Programming

In most cases, these methods wrap and use the method of the same name from scipy.optimize, or use scipy.optimize.minimize with the same method argument.
Thus `leastsq‘ will use scipy.optimize.leastsq, while ‘powell‘ will use scipy.optimize.minimizer(…., method=’powell’)

For more details on the fitting methods please refer to the SciPy docs.